Full Format vs S35 Depth of Field Depth of Field
or
“By how much do we have to increase the lens aperture filming on a small camera format to maintain the same Depth of Field as a lens filming on a large camera format ?”
by Jonathan Maxwell, Optical Designer
Everybody “knows” that the larger the camera detector you use the smaller the Depth of Field will be, right? Why is this so? And is it so?
It is so, and here I try to demystify this. The question is simple to ask, and relatively simple to answer, but as so often happens, what follows will look somewhat complicated. Please bear with me, I’ve worked hard to try and make it clear! To do this, for example, I’ve cut a corner or two in the way I’ve calculated the Depths of Field here, If you’ve ever calculated Depth of Field accurately you will recognise these bruised corners, but cutting these corners does make things easier to understand.
Just in case you forgot: Depth of Field is the distance between the nearest and the farthest objects in a scene that is deemed by the DP, the Camera Operator and the AC to be in focus.
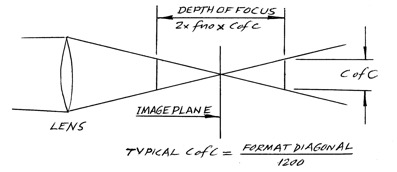
And the Depth of Focus is the distance that a camera technician could move the sensor or image plane (if he or she could) forwards or backwards in the camera without seeing much deterioration in focus quality.
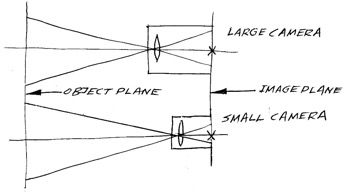
Consider two cameras, one large, and one small, for example:
A “Full Format” 35mm Film camera (36mm x 24mm, format diagonal = 43.27mm, aka “Visatvisionish”) and
A “Super35” 35mm Film camera (24mm x 18mm, format diagonal = 30mm),
both with the same f-no (or T-Stop), the same angular Field of View, and the same focusing distance.
These two cameras are just a simple scaling of each other: the Full Format 35mm Film camera is 43.27mm / 30mm = 1.442 times bigger than the Super35 Film camera, and vice versa.
Let’s take the focal length of the lens of the larger camera to be 50mm, and then the focal length of the lens of the smaller camera will be
50mm /1.442 = 34.67mm, in order to give it the same field angle (angle of view).
Also, let’s assume that the larger camera is working at a magnification of 1/100 , that is, if we consider it as a projector, its magnification is 100x, so the distance to the object (the actors) is 100 x 50mm = 5m, while the smaller camera will then have a magnification of 5m / 34.67mm = 144.2x.
And arbitrarily (as they say) we’ll assume that the two cameras are working at T-4.0
(it doesn’t matter what T-no we use, but 4.0 is just a nice round number)
The Depth of Field in each case is calculated by “projecting” the Depth of Focus out from the camera into “object space” (the place where the actors are), so the smaller camera will have a greater Depth of Field than the larger camera, because the object (the actors, if there are any) is/are relatively further away for the smaller camera than they are for the larger camera.
That’s sort of intuitive, isn’t it? But if you look a bit more closely at this you will see that the Depth of Focus is smaller in the small camera…and this reduces its projected Depth of Field. BUT the magnification of this projection by the smaller camera is greater than for the larger camera, AND it’s not just the regular magnification that the camera is working at that applies here (the size of the object divided by the size of the image), but the SQUARE of that magnification. Longitudinal magnification (which is what applies here) is always the square of the regular magnification, believe me.
The Arithmetic: We now need to get closer to the arithmetic of this projection of the Depth of Focus. To do this we first of all need to look closely at the anatomy of the Depth of Focus:
Yes, the Depth of Focus = 2 x T-stop x CofC, where CofC is the diameter of the Circle of Confusion, which is (typically) taken as: the Camera Format Diagonal /1200 (for the small camera that’s 0.025mm, and for the large camera it’s 0.036mm)
Therefore,
The Depth of Field of the large camera =
2 x 4.0 x 0.036mm x 1002 = 2880mm
And the Depth of Field for the small camera =
2 x 4.0 x 0.025mm x 144.22 = 4159mm
(That’s a lot of Depth of Field, right?)
So now then, what f-no does the smaller camera need to have if we want the Depth of Field to be the same for both cameras?
Call that smaller camera T-stop “X” and then we have, for the smaller camera:
2 x X x 0.025mm x 144.22 = 2880mm (this is the ”required” Depth of Field)
Therefore (with a tiny bit of algebraic manipulation)
X = 2.77, which is the required T-stop for the small camera, and that is 1.06 stops faster than the T-4.0
The above derivation has been spelled out in somewhat awful detail, but looking at the last paragraph, you can see that it can be boiled down to the following simple practical calculation:
If the smaller camera is N times smaller than the larger camera, then:
The smaller camera’s T-stop to achieve the same
Depth of Field as the larger camera = the larger camera’s T-stop / N,
And, practically, it’s just the same with f-nos:
the answer is the larger camera’s f-no / N
So what’s this in Stops ?
Um…. Oh dear, we have to realise that, inconveniently, because f stops and T stops work in a logarithmic way, it’s necessary to use the following formula for this:
The number of stops our smaller camera has to open its iris by is
= 6.644 x (log10 4.0 – log10 2.77) = +1.06 stops
Or, if we use Napierian (aka “natural”) logarithms,
The number of stops increase = 2.885 x (loge 4.0 – loge 2.77) = +1.06 stops
These two funny numbers 6.644 and 2.885 arise because the number of stops down from T-1.0 that any T-stop no is is (I love two ises) given by 2 x logB f-no / logB 2, where B is, guess what, the Base that the logs are based on (incidentally that’s a very useful formula, worth remembering). So whether you use “common” Logs or “natural” Logs there is a 2/log2 multiplier, and that works out to be 6.644 for common logs and 2.885 for natural logs.
Alexa LF vs Super35
OK, while we’re here, the above was for standard Full Format 36 x 24 mm compared with Super 35mm; but what about the new Alexa LF? Alexa LF has a VistaVisionish sensor that is 36.70mm wide x 25.54mm high, with an image diagonal of 44.71mm. How does that compare to using a Super 35mm, 24x18mm, 30mm diagonal?
N = 44.71mm /30mm = 1.49
And if the larger camera has an f-no (or a T-stop) of 5.6 (actually 5.657, right?) the smaller camera will require a T-stop of
5.657 / 1.49 = 3.797
Which is how many stops faster?
Answer = 6.644 x (log10 5.657 – log10 3.797) = +1.15 stops faster
Alexa 65 vs Alexa LF
Oh, alright, now let’s compare the new ALEXA 65 (54.12 mm x 25.58 mm, diagonal = 59.86 mm) with the new Alexa LF (36.70mm wide x 25.54mm high, image diagonal of 44.71mm)
N = 59.86mm /44.71mm = 1.339
And if the larger camera has an f-no (or a T-stop) of 5.6 (actually 5.657, right?) the smaller camera will require an f-no of
5.657 / 1.339 = 4.225
Which is how many stops faster?
Answer = 6.644 x (log10 5.657 – log10 4.225) = +0.842 stop faster
Super35 vs Super16
And finally, let’s take another case: If the larger camera is a Super 35mm cine camera with, of course, an 18mm x 24mm detector (diagonal = 30mm), and the smaller camera is a Super16 camera with a 7.5mm x 12.4mm film gate (diagonal = 14.49mm), then
N = 30mm /14.49mm = 2.07
And if the larger camera has an f-no (or a T-stop) of 5.6 (actually 5.657, right?) the smaller camera will require an f-no of
5.657 / 2.07 = 2.73
Which is how many stops faster?
Answer = 6.644 x (log10 5.657 – log10 2.73) = +2.10 stops faster
END